Calculating the area of a triangle - KS2 Maths

Area of a triangle

To calculate the area of a rectangle you multiply the length by the width.

A right-angled triangle is like half a rectangle.

So to calculate the area of a triangle, you can work out the area of the rectangle and then divide by 2.

The formula for working out the area of a right-angled triangle is:

\(\frac{base × height}{2}\)

Find out how much you know about this topic already with this quiz, then complete the rest of the guide and see if you can beat your score.

Look at this rectangle. It has a width of 8cm and a height of 5cm.

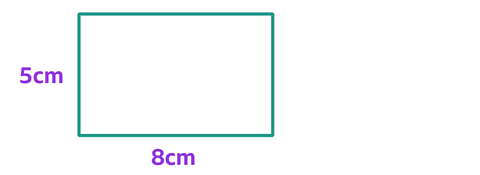
To calculate the area of a rectangle, you multiply the length by the width.

5cm × 8cm = 40cm²

Remember, area is measured in square units, such as square centimetres (cm²) and square metres (m²).

So this rectangle has an area of 40cm².

If you divide this rectangle in two, you can see it creates a right-angled triangle.

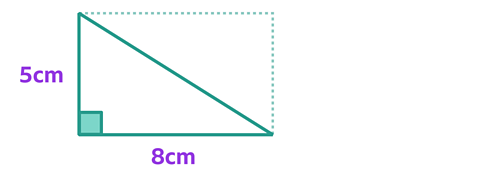
You can see that the area of the right-angled triangle is half the area of the rectangle.

So you could divide the area of the rectangle you calculated above by 2.

40cm² ÷ 2 = 20cm²

The area of this triangle is 20cm².

To calculate the area of a triangle, multiply the base by the height, then divide by 2.

You can write this as a formula:

\(Area = \frac{base × height}{2}\)

Or this could be written in an even simpler way like this:

\(A = \frac{b × h}{2}\)

Let's use this formula to work out the area of this triangle.

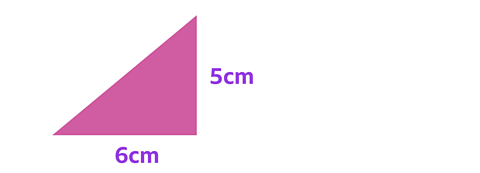
Let’s put in the measurements for the base and height into the formula.

\(\frac{6cm × 5cm}{2}\)

6 multiplied by 5 is 30. You then need to divide 30 by 2.

\(\frac{30}{2} =15cm²\)

Therefore, the area of this triangle is 15cm²

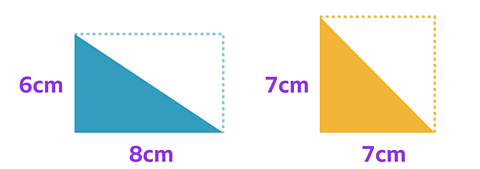
Kevin thinks these two triangles have the same area.

Calculate the area of each and compare them. Is Kevin correct?